Losmalar uchun intervallarni kamaytirish. O'sish va kamaytirish funktsiyalari, ekstremal

O'sish va kamaytirish funktsiyasi

funktsiyasi y = f(x) oraliqda ortish deyiladi [ a, b], agar har qanday juft nuqta uchun X Va X", a ≤ x tengsizlik amal qiladi f(x) ≤ f (x"), va qat'iy ortib borayotgan - tengsizlik bo'lsa f (x) f(x"). Kamaytiruvchi va qat’iy kamayuvchi funksiyalar ham xuddi shunday aniqlanadi. Masalan, funktsiya da = X 2 (guruch. , a) segmentida qat'iy ortadi , va

(guruch. , b) bu ​​segmentda qat'iy kamayadi. Ko'paytirish funktsiyalari belgilangan f (x) va kamayadi f (x)↓. Differensiallanuvchi funksiya uchun f (x) segmentida ortib bordi [ A, b], uning hosilasi zarur va yetarli f"(x) [ da salbiy emas edi A, b].

Segmentdagi funksiyaning ortishi va kamayishi bilan bir qatorda nuqtadagi funksiyaning ortishi va kamayishini ham ko‘rib chiqamiz. Funktsiya da = f (x) nuqtada ortish deyiladi x 0 nuqtani o'z ichiga olgan interval (a, b) bo'lsa x 0, bu har qanday nuqta uchun X dan (a, b), x> x 0 bo'lsa, tengsizlik o'rinli f (x 0) ≤ f (x) va har qanday nuqta uchun X dan (a, b), x 0, tengsizlik o'rinli f (x) ≤ f (x 0). Funktsiyaning nuqtadagi qat'iy ortishi ham xuddi shunday aniqlanadi x 0 . Agar f"(x 0) > 0, keyin funksiya f(x) nuqtada qat'iy ravishda ortadi x 0 . Agar f (x) intervalning har bir nuqtasida ortadi ( a, b), keyin bu oraliqda ortadi.

S. B. Stechkin.

Buyuk Sovet Entsiklopediyasi. - M.: Sovet Entsiklopediyasi. 1969-1978 .

Boshqa lug'atlarda "O'sish va kamaytirish funktsiyalari" nima ekanligini ko'ring:

Matematik analiz tushunchalari. f(x) funksiyasi aholining turli yosh guruhlari sonining AHOLINING YOSH TUZILISHI segmentida ortib borayotgan nisbati deyiladi. Tug'ilish va o'lim darajasiga, odamlarning umr ko'rish davomiyligiga bog'liq ... Katta ensiklopedik lug'at

Matematik analiz tushunchalari. f(x) funksiya segmentda ortib borayotgan deyiladi, agar x1 va x2 nuqtalar juftligi uchun a≤x1 ... ensiklopedik lug'at

Matematika tushunchalari. tahlil. f(x) funksiya chaqiriladi. [a, b] segmentida ortib borish, agar x1 va x2 nuqtalarining har qanday juftligi uchun va<или=х1 <х<или=b, выполняется неравенство f(x1)Tabiiy fan. ensiklopedik lug'at

Funksiyalarning hosilalari va differentsiallari hamda ularning funksiyalarni oʻrganishda qoʻllanilishini oʻrganuvchi matematikaning boʻlimi. D. dizayni va. mustaqil matematik intizomga I. Nyuton va G. Leybnits nomlari bilan bog'liq (17 ning ikkinchi yarmi ... Buyuk Sovet Entsiklopediyasi

Matematikaning hosila va differensial tushunchalari va ularning funksiyalarni oʻrganishda qoʻllanilishi oʻrganiladigan boʻlimi. D. rivojlanishi va. integral hisobining rivojlanishi bilan chambarchas bog'liq. Ularning mazmuni ham ajralmasdir. Ular birgalikda asosni tashkil qiladi ... ... Matematik entsiklopediya

Bu atama boshqa maʼnolarga ham ega, funksiyaga qarang. "Displey" so'rovi bu erda qayta yo'naltiriladi; boshqa maʼnolarga ham qarang... Vikipediya

Aristotel va peripatetiklar- Aristotelning savoli Aristotelning hayoti Aristotel 384/383 yilda tug'ilgan. Miloddan avvalgi e. Stagira shahrida, Makedoniya bilan chegarada. Uning otasi Nikomax Filippning otasi Makedoniya qiroli Amintasning xizmatida shifokor bo'lgan. Oilasi bilan yosh Aristotel... ... G'arb falsafasi o'zining kelib chiqishidan hozirgi kungacha

- (QCD), kvant tasvirida qurilgan kvarklar va glyuonlarning kuchli o'zaro ta'sirining kvant maydoni nazariyasi. "rangli" o'lchov simmetriyasiga asoslangan elektrodinamika (QED). QED dan farqli o'laroq, QCDdagi fermionlar bir-birini to'ldiruvchi xususiyatlarga ega. erkinlikning kvant darajasi raqam, …… Jismoniy ensiklopediya

I Yurak Yurak (lotincha kor, yunoncha cardia) - ichi bo'sh tolali mushak organi bo'lib, nasos vazifasini bajarib, qon aylanish tizimida qon harakatini ta'minlaydi. Anatomiya Yurak oldingi mediastinada (Mediastinum) perikardda... ... orasida joylashgan. Tibbiy ensiklopediya

O'simlik hayoti, boshqa tirik organizmlar kabi, o'zaro bog'liq jarayonlarning murakkab majmuidir; Ulardan eng muhimi, ma'lumki, atrof-muhit bilan moddalar almashinuvidir. Atrof-muhit - bu manba ... ... Biologik ensiklopediya

Funktsiyaning ekstremal qismi

Ta'rif 2

$x_0$ nuqtasi $f(x)$ funksiyaning maksimal nuqtasi deyiladi, agar shu nuqtaning shunday qo'shnisi bo'lsaki, shu qo'shnilikdagi barcha $x$ uchun $f(x)\le f(x_0) tengsizlik bo'lsin. $ ushlab turadi.

Ta'rif 3

$x_0$ nuqtasi $f(x)$ funksiyaning maksimal nuqtasi deyiladi, agar shu nuqtaga shunday qo'shni bo'lsaki, shu qo'shnilikdagi barcha $x$lar uchun $f(x)\ge f(x_0) tengsizlik bo'lsin. $ ushlab turadi.

Funksiyaning ekstremum tushunchasi funksiyaning kritik nuqtasi tushunchasi bilan chambarchas bog‘liq. Keling, uning ta'rifini keltiramiz.

Ta'rif 4

$x_0$ $f(x)$ funksiyasining kritik nuqtasi deyiladi, agar:

1) $x_0$ - aniqlash sohasining ichki nuqtasi;

2) $f"\left(x_0\right)=0$ yoki mavjud emas.

Ekstremum tushunchasi uchun biz uning mavjudligi uchun etarli va zarur shartlar haqida teoremalarni shakllantirishimiz mumkin.

Teorema 2

Ekstremum uchun etarli shart

$x_0$ nuqtasi $y=f(x)$ funksiyasi uchun kritik bo‘lsin va $(a,b)$ oralig‘ida yotsin. Har bir $\left(a,x_0\right)\ va \ (x_0,b)$ oralig'ida $f"(x)$ hosilasi mavjud bo'lsin va doimiy belgini saqlab tursin. Keyin:

1) Agar $(a,x_0)$ oralig'ida hosila $f"\left(x\right)>0$ bo'lsa va $(x_0,b)$ oralig'ida hosila $f"\left( bo'lsa. x\o'ng)

2) Agar $(a,x_0)$ oralig'ida $f"\left(x\right)0$ hosilasi bo'lsa, u holda $x_0$ nuqtasi bu funksiya uchun minimal nuqta hisoblanadi.

3) $(a,x_0)$ oralig'ida va $(x_0,b)$ oralig'ida $f"\left(x\right) >0$ hosilasi yoki $f"\left(x) hosilasi bo'lsa \o'ng)

Bu teorema 1-rasmda tasvirlangan.

Shakl 1. Ekstremaning mavjudligi uchun etarli shart

Ekstremallarga misollar (2-rasm).

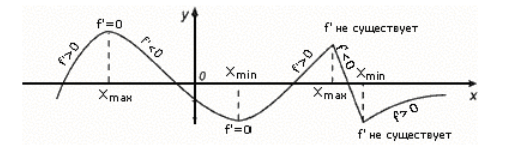
Shakl 2. Ekstremal nuqtalarga misollar

Ekstremum uchun funktsiyani o'rganish qoidasi

2) $f"(x)$ hosilasini toping;

7) 2-teoremadan foydalanib, har bir oraliqda maksimal va minimallarning mavjudligi haqida xulosa chiqaring.

O'sish va kamaytirish funktsiyasi

Keling, birinchi navbatda o'suvchi va kamayuvchi funktsiyalarning ta'riflari bilan tanishamiz.

Ta'rif 5

$X$ oraliqda aniqlangan $y=f(x)$ funksiya, agar X$ dagi $x_1,x_2\ nuqtalari uchun $x_1 boʻlsa, ortib borayotgan deyiladi.

Ta'rif 6

$X$ oraliqda aniqlangan $y=f(x)$ funksiyasi $x_1f(x_2)$ uchun X$da $x_1,x_2\ har qanday nuqtalar uchun kamayuvchi deyiladi.

O'sish va kamaytirish funksiyasini o'rganish

Siz hosila yordamida ortib borayotgan va kamayuvchi funksiyalarni o'rganishingiz mumkin.

Funktsiyani o'sish va kamaytirish oraliqlari uchun tekshirish uchun siz quyidagilarni bajarishingiz kerak:

1) $f(x)$ funksiyaning aniqlanish sohasini toping;

2) $f"(x)$ hosilasini toping;

3) $f"\left(x\right)=0$ tengligi bajariladigan nuqtalarni toping;

4) $f"(x)$ mavjud bo'lmagan nuqtalarni toping;

5) Koordinata chizig'ida barcha topilgan nuqtalarni va ushbu funktsiyaning aniqlanish sohasini belgilang;

6) Har bir natijaviy intervalda $f"(x)$ hosilasining belgisini aniqlang;

7) Xulosa chiqaring: $f"\left(x\right)0$ oraliqlarda funktsiya ortib boradi.

Ekstremal nuqtalarning ortishi, kamayishi va mavjudligi funktsiyalarini o'rganish masalalariga misollar

1-misol

Funktsiyani oshirish va kamaytirish, maksimal va minimal nuqtalar mavjudligini tekshiring: $f(x)=(2x)^3-15x^2+36x+1$

Dastlabki 6 ball bir xil bo'lgani uchun, avval ularni bajaramiz.

1) Aniqlash sohasi - barcha haqiqiy sonlar;

2) $f"\left(x\right)=6x^2-30x+36$;

3) $f"\left(x\right)=0$;

\ \ \

4) $f"(x)$ ta'rif sohasining barcha nuqtalarida mavjud;

5) Koordinatali chiziq:

3-rasm.

6) Har bir intervalda $f"(x)$ hosilasining belgisini aniqlang:

\ \ .

Funksiyaning ekstremumi uchun yetarli shartlar.

Funksiyaning maksimal va minimasini topish uchun ekstremumning uchta belgisidan istalganidan foydalanish mumkin, albatta, agar funksiya ularning shartlarini qanoatlantirsa. Eng keng tarqalgan va qulay - ulardan birinchisi.

Ekstremum uchun birinchi etarli shart.

y=f(x) funksiya nuqtaning -qo‘shnisida differensiallanuvchi va nuqtaning o‘zida uzluksiz bo‘lsin.

Boshqa so'z bilan:

Funksiya ekstremumining birinchi belgisi asosida ekstremum nuqtalarini topish algoritmi.

• Funktsiyani aniqlash sohasini topamiz.
• Funktsiyaning hosilasini aniqlanish sohasi bo'yicha topamiz.
• Numeratorning nollarini, hosila maxrajining nollarini va hosila mavjud bo'lmagan ta'rif sohasining nuqtalarini aniqlaymiz (barcha sanab o'tilgan nuqtalar deyiladi) mumkin bo'lgan ekstremal nuqtalar, bu nuqtalardan o'tib, hosila faqat o'z belgisini o'zgartirishi mumkin).
• Bu nuqtalar funktsiyani aniqlash sohasini hosila o'z belgisini saqlaydigan intervallarga ajratadi. Har bir oraliqda hosilaning belgilarini aniqlaymiz (masalan, ma'lum bir oraliqning istalgan nuqtasida funktsiya hosilasining qiymatini hisoblash yo'li bilan).
• Biz funktsiya uzluksiz bo'lgan nuqtalarni tanlaymiz va u orqali lotin belgisi o'zgaradi - bu ekstremal nuqtalar.

Juda koʻp soʻzlar bor, keling, funksiya ekstremumining birinchi yetarli shartidan foydalanib, funksiyaning ekstremum nuqtalari va ekstremallarini topishning bir nechta misollarini koʻrib chiqaylik.

Misol.

Funksiyaning ekstremal qismini toping.

Yechim.

Funksiyaning sohasi x=2 dan tashqari haqiqiy sonlarning butun to‘plamidir.

Hosilini topish:

Numeratorning nollari x=-1 va x=5 nuqtalari bo'lib, x=2 da maxraj nolga tushadi. Ushbu nuqtalarni raqamlar o'qida belgilang

Har bir oraliqda hosilaning belgilarini aniqlaymiz, buning uchun hosila qiymatini har bir intervalning istalgan nuqtasida, masalan, x=-2, x=0, x=3 va nuqtalarda hisoblaymiz. x=6.

Shuning uchun, intervalda hosila ijobiy bo'ladi (rasmda biz bu oraliq ustiga ortiqcha belgisi qo'yamiz). Xuddi shunday

Shuning uchun biz ikkinchi oraliqdan minusni, uchinchidan minusni va to'rtinchidan ortiqcha qo'yamiz.

Funktsiya uzluksiz bo'lgan va uning hosilasi belgisini o'zgartiradigan nuqtalarni tanlash qoladi. Bu ekstremal nuqtalar.

Shu nuqtada x=-1 funksiya uzluksiz va hosila belgisi plyusdan minusga o'zgaradi, shuning uchun ekstremumning birinchi belgisiga ko'ra, x=-1 maksimal nuqta, funktsiyaning maksimali unga mos keladi. .

Shu nuqtada x=5 funksiya uzluksiz va hosila belgisini minusdan plyusga o'zgartiradi, shuning uchun x=-1 minimal nuqta, funktsiyaning minimumi unga mos keladi. .

Grafik illyustratsiya.

Javob:

DIQQAT: ekstremum uchun birinchi yetarli mezon funksiyaning nuqtadagi farqlanishini talab qilmaydi.

Misol.

Funksiyaning ekstremum nuqtalari va ekstremallarini toping .

Yechim.

Funksiya sohasi haqiqiy sonlarning butun to‘plamidir. Funktsiyaning o'zi quyidagicha yozilishi mumkin:

Funktsiyaning hosilasini topamiz:

Shu nuqtada x=0 hosila mavjud emas, chunki argument nolga intilganda bir tomonlama chegaralarning qiymatlari mos kelmaydi:

Shu bilan birga, asl funktsiya x=0 nuqtada uzluksizdir (uzluksizlik uchun funktsiyani o'rganish bo'limiga qarang):

Keling, hosila nolga tushadigan argumentning qiymatini topamiz:

Olingan barcha nuqtalarni raqamlar chizig'ida belgilaymiz va har bir intervalda hosila belgisini aniqlaymiz. Buning uchun biz lotin qiymatlarini har bir intervalning ixtiyoriy nuqtalarida hisoblaymiz, masalan, x=-6, x=-4, x=-1, x=1, x=4, x=6.

Ya'ni,

Shunday qilib, ekstremumning birinchi belgisiga ko'ra, minimal nuqtalar , maksimal ball .

Funktsiyaning mos keladigan minimalini hisoblaymiz

Funktsiyaning mos keladigan maksimallarini hisoblaymiz

Grafik illyustratsiya.

Javob:

.

Funksiya ekstremumining ikkinchi belgisi.

Ko'rib turganingizdek, funksiya ekstremumining bu belgisi nuqtada hech bo'lmaganda ikkinchi tartibli hosilaning mavjudligini talab qiladi.

Grafikdan kvadratik funktsiyaning ortish va kamayish oraliqlarini topish xy 0 11 Agar x ning kattaroq qiymati y ning kichik qiymatiga to'g'ri kelsa, funktsiya intervalda kamayib boradi, ya'ni chapdan o'ngga harakatlanayotganda grafik pastga tushadi ( Ko'rish uchun bosing) Agar kattaroq x qiymati kattaroq y qiymatiga to'g'ri keladigan bo'lsa, funktsiya intervalda ortib bormoqda, ya'ni chapdan o'ngga harakatlanayotganda grafik yuqoriga ko'tariladi (ko'rish uchun bosing)

8 y x0 11 Grafikdan toping va kvadrat funktsiyaning o'sish va kamayish oraliqlarini yozing.E'tibor bering, kvadrat funktsiyaning grafigi ikkita shoxdan iborat. Tarmoqlar bir-biri bilan parabola cho'qqisi orqali bog'langan. O'sish va kamayish oraliqlarini qayd etishda eng muhim rolni parabolaning uchlari abssissasi (x) o'ynaydi.1-misol.Parabolaning har bir tarmog'i bo'ylab harakatni alohida ko'rib chiqamiz: chap novda bo'ylab, harakatlanayotganda. chapdan o'ngga qarab, grafik pastga tushadi, ya'ni funksiya kamayadi; o'ng filial bo'ylab - grafik yuqoriga ko'tariladi, ya'ni funktsiya ortib bormoqda. Javob: kamayuvchi interval (- ∞; -1 ]; ortib boruvchi interval [ -1; +∞)

8 y x0 11 Grafikdan toping va kvadrat funktsiyaning ortish va kamayish oraliqlarini yozing 2-misol. Parabolaning har bir shoxi bo'ylab harakatni alohida ko'rib chiqing: chap shox bo'ylab, chapdan o'ngga harakat qilganda, grafik ketadi. yuqoriga, ya'ni funktsiya oshadi; o'ng filial bo'ylab - grafik pastga tushadi, bu funktsiyaning kamayishini bildiradi. Javob: o'sish oralig'i (- ∞; 3 ]; pasayish oralig'i [ 3; +∞).

Mustaqil yechish uchun topshiriqlar (daftarda bajarilishi kerak) 1-topshiriq 2-topshiriq 3-topshiriq 4-ilova

ortib boruvchi interval (- ∞; -1 ]; kamayuvchi interval [ -1; +∞). javobni tekshiring. Grafikdan toping va kvadratik funktsiyaning ortish va kamayish oraliqlarini yozing 88 y x0 1 11 animatsiyani tomosha qiling javobni o'zingiz yozing

“kamayuvchi interval (- ∞; 3 ]; ortib boruvchi interval [ 3; +∞). Grafikdan toping va kvadratik funktsiyaning ortishi va kamayishi oraliqlarini yozing y x 11 0 8 2 animatsiyani tomosha qiling javobni yozing javobni o'zingiz tekshiring

Grafikdan toping va kvadrat funktsiyaning o'sish va kamayish oraliqlarini yozing 8 y 0 1 1 x3 animatsiyani ko'ring, javobni o'zingiz yozing pasayish intervalini (- ∞; 0 ]; o'sish oralig'i [ 0; +∞ ). javobni tekshiring

“Grafikdan toping va kvadrat funktsiyaning ortish va kamayish oraliqlarini yozing 8 1 y 01 x4 animatsiyani ko'ring, javobni o'zingiz yozing oshirish oralig'ini (- ∞; - 0. 5 ]; kamayish oralig'i [ - 0. 5; + ∞). javobni tekshiring

Ilova O'sish va kamayish oraliqlarining chegara nuqtasi parabola cho'qqisining abssissasidir.Kadratik funktsiya uzluksiz bo'lganligi uchun javobda o'sish va kamayish oraliqlarining chegara nuqtasi har doim kvadrat qavs bilan yoziladi.

Funktsiyaning ekstremal qismi

Ta'rif 2

$x_0$ nuqtasi $f(x)$ funksiyaning maksimal nuqtasi deyiladi, agar shu nuqtaning shunday qo'shnisi bo'lsaki, shu qo'shnilikdagi barcha $x$ uchun $f(x)\le f(x_0) tengsizlik bo'lsin. $ ushlab turadi.

Ta'rif 3

$x_0$ nuqtasi $f(x)$ funksiyaning maksimal nuqtasi deyiladi, agar shu nuqtaga shunday qo'shni bo'lsaki, shu qo'shnilikdagi barcha $x$lar uchun $f(x)\ge f(x_0) tengsizlik bo'lsin. $ ushlab turadi.

Funksiyaning ekstremum tushunchasi funksiyaning kritik nuqtasi tushunchasi bilan chambarchas bog‘liq. Keling, uning ta'rifini keltiramiz.

Ta'rif 4

$x_0$ $f(x)$ funksiyasining kritik nuqtasi deyiladi, agar:

1) $x_0$ - aniqlash sohasining ichki nuqtasi;

2) $f"\left(x_0\right)=0$ yoki mavjud emas.

Ekstremum tushunchasi uchun biz uning mavjudligi uchun etarli va zarur shartlar haqida teoremalarni shakllantirishimiz mumkin.

Teorema 2

Ekstremum uchun etarli shart

$x_0$ nuqtasi $y=f(x)$ funksiyasi uchun kritik bo‘lsin va $(a,b)$ oralig‘ida yotsin. Har bir $\left(a,x_0\right)\ va \ (x_0,b)$ oralig'ida $f"(x)$ hosilasi mavjud bo'lsin va doimiy belgini saqlab tursin. Keyin:

1) Agar $(a,x_0)$ oralig'ida hosila $f"\left(x\right)>0$ bo'lsa va $(x_0,b)$ oralig'ida hosila $f"\left( bo'lsa. x\o'ng)

2) Agar $(a,x_0)$ oralig'ida $f"\left(x\right)0$ hosilasi bo'lsa, u holda $x_0$ nuqtasi bu funksiya uchun minimal nuqta hisoblanadi.

3) $(a,x_0)$ oralig'ida va $(x_0,b)$ oralig'ida $f"\left(x\right) >0$ hosilasi yoki $f"\left(x) hosilasi bo'lsa \o'ng)

Bu teorema 1-rasmda tasvirlangan.

Shakl 1. Ekstremaning mavjudligi uchun etarli shart

Ekstremallarga misollar (2-rasm).

Shakl 2. Ekstremal nuqtalarga misollar

Ekstremum uchun funktsiyani o'rganish qoidasi

2) $f"(x)$ hosilasini toping;

7) 2-teoremadan foydalanib, har bir oraliqda maksimal va minimallarning mavjudligi haqida xulosa chiqaring.

O'sish va kamaytirish funktsiyasi

Keling, birinchi navbatda o'suvchi va kamayuvchi funktsiyalarning ta'riflari bilan tanishamiz.

Ta'rif 5

$X$ oraliqda aniqlangan $y=f(x)$ funksiya, agar X$ dagi $x_1,x_2\ nuqtalari uchun $x_1 boʻlsa, ortib borayotgan deyiladi.

Ta'rif 6

$X$ oraliqda aniqlangan $y=f(x)$ funksiyasi $x_1f(x_2)$ uchun X$da $x_1,x_2\ har qanday nuqtalar uchun kamayuvchi deyiladi.

O'sish va kamaytirish funksiyasini o'rganish

Siz hosila yordamida ortib borayotgan va kamayuvchi funksiyalarni o'rganishingiz mumkin.

Funktsiyani o'sish va kamaytirish oraliqlari uchun tekshirish uchun siz quyidagilarni bajarishingiz kerak:

1) $f(x)$ funksiyaning aniqlanish sohasini toping;

2) $f"(x)$ hosilasini toping;

3) $f"\left(x\right)=0$ tengligi bajariladigan nuqtalarni toping;

4) $f"(x)$ mavjud bo'lmagan nuqtalarni toping;

5) Koordinata chizig'ida barcha topilgan nuqtalarni va ushbu funktsiyaning aniqlanish sohasini belgilang;

6) Har bir natijaviy intervalda $f"(x)$ hosilasining belgisini aniqlang;

7) Xulosa chiqaring: $f"\left(x\right)0$ oraliqlarda funktsiya ortib boradi.

Ekstremal nuqtalarning ortishi, kamayishi va mavjudligi funktsiyalarini o'rganish masalalariga misollar

1-misol

Funktsiyani oshirish va kamaytirish, maksimal va minimal nuqtalar mavjudligini tekshiring: $f(x)=(2x)^3-15x^2+36x+1$

Dastlabki 6 ball bir xil bo'lgani uchun, avval ularni bajaramiz.

1) Aniqlash sohasi - barcha haqiqiy sonlar;

2) $f"\left(x\right)=6x^2-30x+36$;

3) $f"\left(x\right)=0$;

\ \ \

4) $f"(x)$ ta'rif sohasining barcha nuqtalarida mavjud;

5) Koordinatali chiziq:

3-rasm.

6) Har bir intervalda $f"(x)$ hosilasining belgisini aniqlang:

\ \}